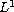 -data
-data
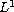 -data
-data
Alexander A. Kovalevsky, Yuliya S. Gorban
Abstract:
In this article, we study the Dirichlet problem for degenerate anisotropic
elliptic second-order equations with
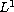 -right-hand sides on a
bounded open set of
-right-hand sides on a
bounded open set of
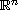 (
(
 ).
These equations are described with a set of exponents and of a set of
weighted functions. The exponents characterize the rates of growth of the
coefficients of the equations with respect to the corresponding derivatives
of the unknown function, and the weighted functions characterize
degeneration or singularity of the coefficients of the equations with
respect to the spatial variable.
We prove theorems on the existence of entropy solutions, T-solutions,
W-solutions, and weighted weak solutions of the problem under consideration.
).
These equations are described with a set of exponents and of a set of
weighted functions. The exponents characterize the rates of growth of the
coefficients of the equations with respect to the corresponding derivatives
of the unknown function, and the weighted functions characterize
degeneration or singularity of the coefficients of the equations with
respect to the spatial variable.
We prove theorems on the existence of entropy solutions, T-solutions,
W-solutions, and weighted weak solutions of the problem under consideration.
Submitted November 28, 2012. Published July 22, 2013.
Math Subject Classifications: 35J25, 35J60, 35J70, 35R05.
Key Words: Degenerate anisotropic elliptic second-order equations;
L1-data; Dirichlet problem; entropy solution; T-solution;
W-solution; weighted weak solution; existence of solutions.
Show me the PDF file (314 KB), TEX file, and other files for this article.
 |
Alexander A. Kovalevsky Department of Nonlinear Analysis Institute of Applied Mathematics and Mechanics National Academy of Sciences of Ukraine, Donetsk, Ukraine email: alexkvl@iamm.ac.donetsk.ua |
|---|---|
 |
Yuliya S. Gorban Department of Differential Equations Donetsk National University, Donetsk, Ukraine email: yuliya_gorban@mail.ru |
Return to the EJDE web page