Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 163, pp. 1-13.
Properties of solutions of fourth-order nonlinear evolution equations
Ning Duan, Xiaopeng Zhao, Bo Liu
Abstract:
In this article, we consider the existence and uniqueness of global
solutions for a fourth-order nonlinear evolution equation which
models the formation of facets and corners in the course of kinetically
controlled crystal growth. Moreover, the existence of global attractor
in
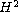 and
and
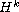
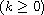 space is also considered.
space is also considered.
Submitted August 24, 2012. Published July 19, 2013.
Math Subject Classifications: 35B41, 35K55.
Key Words: Fourth-order nonlinear evolution equation; existence;
uniqueness; global attractor.
Show me the PDF file (243 KB),
TEX file, and other files for this article.
 |
Ning Duan
College of Mathematics, Jilin University
Changchun 130012, China
email: 123332453@qq.com
|
|---|
 |
Xiaopeng Zhao
School of Science, Jiangnan University
Wuxi 214122, China
email: zxp032@126.com
|
|---|
 |
Bo Liu
College of Mathematics, Jilin University
Changchun 130012, China
email: liubom@jlu.edu.cn
|
|---|
Return to the EJDE web page
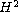 and
and
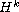
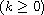 space is also considered.
space is also considered.


