Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 16, pp. 1-14.
Growth and oscillation of differential polynomials generated by
complex differential equations
Zinelaabidine Latreuch, Benharrat Belaidi
Abstract:
The main purpose of this article is to study the controllability
of solutions to the linear differential equation
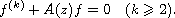
We study the growth and oscillation of higher-order differential
polynomials with meromorphic coefficients generated by solutions
of the above differential equation.
Submitted July 27, 2012. Published January 21, 2013.
Math Subject Classifications: 34M10, 30D35.
Key Words: Linear differential equations; finite order;
hyper-order; sequence of zeros; exponent of convergence;
hyper-exponent of convergence
Show me the PDF file (241 KB),
TEX file, and other files for this article.
 |
Zinelaâbidine Latreuch
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem (UMAB)
B. P. 227 Mostaganem, Algeria
email: z.latreuch@gmail.com
|
|---|
 |
Benharrat Belaïdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem (UMAB)
B. P. 227 Mostaganem, Algeria
email: belaidi@univ-mosta.dz
|
|---|
Return to the EJDE web page