Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 158, pp. 1-12.
Existence of solutions for a Neumann problem involving
the p(x)-Laplacian
Giuseppina Barletta, Antonia Chinni
Abstract:
We study the existence and multiplicity of weak solutions
for a parametric Neumann problem driven by the p(x)-Laplacian.
Under a suitable condition on the behavior of the potential at
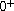 ,
we obtain an interval such that when a parameter
,
we obtain an interval such that when a parameter
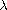 is in this interval, our problem admits at least one nontrivial weak solution.
We show the multiplicity of solutions for potentials
satisfying also the Ambrosetti-Rabinowitz condition. Moreover,
if the right-hand side f satisfies the Ambrosetti-Rabinowitz condition,
then we obtain the existence of two nontrivial weak solutions.
is in this interval, our problem admits at least one nontrivial weak solution.
We show the multiplicity of solutions for potentials
satisfying also the Ambrosetti-Rabinowitz condition. Moreover,
if the right-hand side f satisfies the Ambrosetti-Rabinowitz condition,
then we obtain the existence of two nontrivial weak solutions.
Submitted March 29, 2013. Published July 10, 2013.
Math Subject Classifications: 35J60, 35J20.
Key Words: p(x)-Laplacian; variable exponent Sobolev spaces.
Show me the PDF file (254 KB),
TEX file, and other files for this article.
 |
Giuseppina Barletta
Università degli Studi Mediterranea di Reggio Calabria
MECMAT-Dipartimento di Meccanica e Materiali, Via Graziella
Località Feo di Vito, 89100 Reggio Calabria, Italy
email: giuseppina.barletta@unirc.it
|
|---|
 |
Antonia Chinnì
Department of Civil, Information Technology, Construction,
Environmental Engineering and Applied Mathematics
University of Messina, 98166 Messina, Italy
email: achinni@unime.it
|
|---|
Return to the EJDE web page
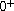 ,
we obtain an interval such that when a parameter
,
we obtain an interval such that when a parameter
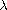 is in this interval, our problem admits at least one nontrivial weak solution.
We show the multiplicity of solutions for potentials
satisfying also the Ambrosetti-Rabinowitz condition. Moreover,
if the right-hand side f satisfies the Ambrosetti-Rabinowitz condition,
then we obtain the existence of two nontrivial weak solutions.
is in this interval, our problem admits at least one nontrivial weak solution.
We show the multiplicity of solutions for potentials
satisfying also the Ambrosetti-Rabinowitz condition. Moreover,
if the right-hand side f satisfies the Ambrosetti-Rabinowitz condition,
then we obtain the existence of two nontrivial weak solutions.

