Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 155, pp. 1-6.
Infinite semipositone problems with indefinite weight
and asymptotically linear growth forcing-terms
Ghasem A. Afrouzi, Saleh Shakeri
Abstract:
In this work, we study the existence of positive solutions to the
singular problem
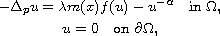
where
 is positive parameter,
is positive parameter,
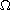 is a bounded domain with smooth boundary,
is a bounded domain with smooth boundary,
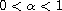 ,
and
,
and
![$ f:[0,\infty] \to\mathbb{R}$](gifs/ae.gif) is a continuous
function which is asymptotically p-linear at
is a continuous
function which is asymptotically p-linear at
 .
The weight function is continuous satisfies
.
The weight function is continuous satisfies
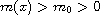 ,
,
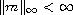 . We prove the existence of a positive solution
for a certain range of
. We prove the existence of a positive solution
for a certain range of
 using the method of sub-supersolutions.
using the method of sub-supersolutions.
Submitted September 17, 2012. Published July 8, 2013.
Math Subject Classifications: 35J55, 35J25.
Key Words: Infinite semipositone problem; indefinite weight; forcing term;
asymptotically linear growth; sub-supersolution method.
Show me the PDF file (193 KB),
TEX file, and other files for this article.
 |
Ghasem Alizadeh Afrouzi
Department of Mathematics, Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Saleh Shakeri
Department of Mathematics
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: s.shakeri@umz.ac.ir
|
|---|
Return to the EJDE web page
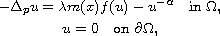
 is positive parameter,
is positive parameter,
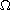 is a bounded domain with smooth boundary,
is a bounded domain with smooth boundary,
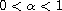 ,
and
,
and
![$ f:[0,\infty] \to\mathbb{R}$](gifs/ae.gif) is a continuous
function which is asymptotically p-linear at
is a continuous
function which is asymptotically p-linear at
 .
The weight function is continuous satisfies
.
The weight function is continuous satisfies
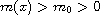 ,
,
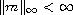 . We prove the existence of a positive solution
for a certain range of
. We prove the existence of a positive solution
for a certain range of
 using the method of sub-supersolutions.
using the method of sub-supersolutions.

