Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 150, pp. 1-21.
Existence of infinitely many periodic subharmonic solutions for
nonlinear non-autonomous neutral differential equations
Xiao-Bao Shu, Yongzeng Lai, Fei Xu
Abstract:
In this article, we study the existence of an infinite number of
subharmonic periodic solutions to a class of second-order neutral
nonlinear functional differential equations. Subdifferentiability
of lower semicontinuous convex functions
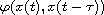 and the corresponding conjugate functions are constructed.
By combining the critical point theory, Z2-group index theory
and operator equation theory, we obtain the infinite number of
subharmonic periodic solutions to such system.
and the corresponding conjugate functions are constructed.
By combining the critical point theory, Z2-group index theory
and operator equation theory, we obtain the infinite number of
subharmonic periodic solutions to such system.
Submitted November 13, 2012. Published June 28, 2013.
Math Subject Classifications: 34K13, 34K40, 65K10.
Key Words: Subharmonic periodic solution; variational structure;
operator equation; critical point; subdifferential;
neutral functional differential equation; Z2-group; index theory.
Show me the PDF file (296 KB),
TEX file, and other files for this article.
 |
Xiao-Bao Shu
Department of Mathematics, Hunan University
Changsha 410082, China
email: sxb0221@163.com
|
|---|
 |
Yongzeng Lai
Department of Mathematics,
Wilfrid Laurier University
Waterloo, Ontario
N2L 3C5, Canada
email: ylai@wlu.ca
|
|---|
 |
Fei Xu
Department of Mathematics
Wilfrid Laurier University
Waterloo, Ontario
N2L 3C5, Canada
email: fxu.feixu@gmail.com
|
|---|
Return to the EJDE web page
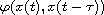 and the corresponding conjugate functions are constructed.
By combining the critical point theory, Z2-group index theory
and operator equation theory, we obtain the infinite number of
subharmonic periodic solutions to such system.
and the corresponding conjugate functions are constructed.
By combining the critical point theory, Z2-group index theory
and operator equation theory, we obtain the infinite number of
subharmonic periodic solutions to such system.


