Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 129, pp. 1-11.
Selfadjoint extensions of a singular multipoint differential operator
of first order
Zameddin I. Ismailov, Rukiye Ozturk Mert
Abstract:
In this work, we describe all selfadjoint extensions of the minimal
operator generated by linear singular multipoint symmetric differential
expression
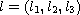 ,
,
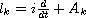 with selfadjoint
operator coefficients
with selfadjoint
operator coefficients
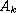 ,
,
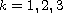 in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
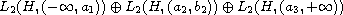
where
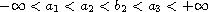 .
Also, we study the structure of the spectrum of these extensions.
.
Also, we study the structure of the spectrum of these extensions.
Submitted April 29, 2013. Published May 27, 2013.
Math Subject Classifications: 47A10, 47A20.
Key Words: Quantum field theory; spectrum; multipoint differential operators;
selfadjoint extension.
Show me the PDF file (214 KB),
TEX file, and other files for this article.
 |
Zameddin I. Ismailov
Department of Mathematics, Faculty of Sciences
Karadeniz Technical University
61080, Trabzon, Turkey
email: zameddin@yahoo.com
|
|---|
 |
Rukiye Ozturk Mert
Department of Mathematics, Art and Science Faculty
Hitit University, 19030, Corum, Turkey
email: rukiyeozturkmert@hitit.edu.tr
|
|---|
Return to the EJDE web page
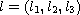 ,
,
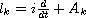 with selfadjoint
operator coefficients
with selfadjoint
operator coefficients
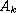 ,
,
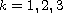 in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
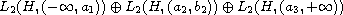
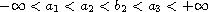 .
Also, we study the structure of the spectrum of these extensions.
.
Also, we study the structure of the spectrum of these extensions.

