Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 117, pp. 1-14.
Direct and inverse bifurcation problems for non-autonomous
logistic equations
Tetsutaro Shibata
Abstract:
We consider the semilinear eigenvalue problem
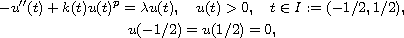
where p > 1 is a constant,
and
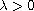 is a parameter. We propose a new
inverse bifurcation problem. Assume that k(t) is an unknown
function. Then can we determine k(t) from the asymptotic behavior of
the bifurcation curve?
The purpose of this paper is to answer this question affirmatively.
The key ingredient is the precise asymptotic formula for
the
is a parameter. We propose a new
inverse bifurcation problem. Assume that k(t) is an unknown
function. Then can we determine k(t) from the asymptotic behavior of
the bifurcation curve?
The purpose of this paper is to answer this question affirmatively.
The key ingredient is the precise asymptotic formula for
the
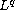 -bifurcation curve
-bifurcation curve
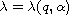 as
as
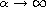 (
(
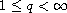 ),
where
),
where
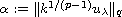 .
.
Submitted December 28, 2012. Published May 10, 2013.
Math Subject Classifications: 34C23, 34B15.
Key Words: Inverse bifurcation problem; non-autonomous equation;
logistic equations.
Show me the PDF file (269 KB),
TEX file, and other files for this article.
 |
Tetsutaro Shibata
Laboratory of Mathematics, Institute of Engineering
Hiroshima University, Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
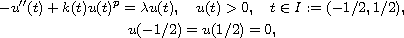
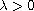 is a parameter. We propose a new
inverse bifurcation problem. Assume that k(t) is an unknown
function. Then can we determine k(t) from the asymptotic behavior of
the bifurcation curve?
The purpose of this paper is to answer this question affirmatively.
The key ingredient is the precise asymptotic formula for
the
is a parameter. We propose a new
inverse bifurcation problem. Assume that k(t) is an unknown
function. Then can we determine k(t) from the asymptotic behavior of
the bifurcation curve?
The purpose of this paper is to answer this question affirmatively.
The key ingredient is the precise asymptotic formula for
the
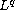 -bifurcation curve
-bifurcation curve
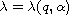 as
as
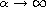 (
(
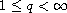 ),
where
),
where
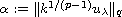 .
.
