Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 109, pp. 1-16.
Existence of solutions for critical elliptic systems with
boundary singularities
Jianfu Yang, Linli Wu
Abstract:
This article concerns the existence of positive solutions to the
nonlinear elliptic system involving critical Hardy-Sobolev exponent

where
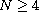 and
and
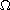 is a
is a
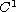 bounded domain in
bounded domain in
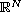 ,
,
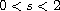 ,
,
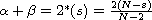 ,
,
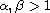 ,
,
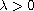 and
and
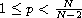 .
.
Let
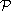 be a linear subspace of
be a linear subspace of
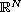 such that
such that
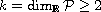 , and
, and
 be the orthogonal
projection on
be the orthogonal
projection on
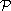 with respect to the Euclidean structure.
We consider mainly the case when
with respect to the Euclidean structure.
We consider mainly the case when
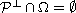 and
and
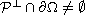 .
We show that there exists
.
We show that there exists
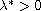 such that the system above
possesses at least one positive solution for
such that the system above
possesses at least one positive solution for
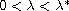 provided that at each point
provided that at each point
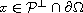 the principal curvatures of
the principal curvatures of
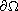 at
at
 are non-positive,
but not all vanish.
are non-positive,
but not all vanish.
Submitted October 16, 2012. Published April 29, 2013.
Math Subject Classifications: 35J25, 25J50, 35J57.
Key Words: Existence; compactness; critical Hardy-Sobolev exponent;
nonlinear system.
Show me the PDF file (273 KB),
TEX file, and other files for this article.
 |
Jianfu Yang
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
| |
Linli Wu
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: llwujxsd@sina.com
|
|---|
Return to the EJDE web page

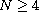 and
and
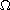 is a
is a
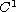 bounded domain in
bounded domain in
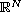 ,
,
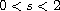 ,
,
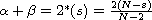 ,
,
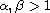 ,
,
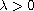 and
and
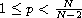 .
. 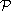 be a linear subspace of
be a linear subspace of
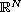 such that
such that
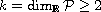 , and
, and
 be the orthogonal
projection on
be the orthogonal
projection on
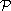 with respect to the Euclidean structure.
We consider mainly the case when
with respect to the Euclidean structure.
We consider mainly the case when
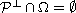 and
and
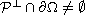 .
We show that there exists
.
We show that there exists
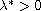 such that the system above
possesses at least one positive solution for
such that the system above
possesses at least one positive solution for
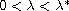 provided that at each point
provided that at each point
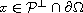 the principal curvatures of
the principal curvatures of
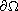 at
at
 are non-positive,
but not all vanish.
are non-positive,
but not all vanish.
