We study the existence of multiple solutions to the boundary value problem
![$$\displaylines{
\frac{d}{dt}\Big(\frac12{}_0D_t^{-\beta}(u'(t))+\frac12{}_tD_T^{-\beta}(u'(t))
\Big)+\lambda \nabla F(t,u(t))=0,\quad t\in [0,T],\cr
u(0)=u(T)=0,
}$$](gifs/aa.gif)
where
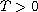 ,
,
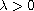 is a parameter,
is a parameter,
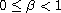 ,
,
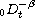 and
and
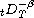 are, respectively, the left and right Riemann-Liouville
fractional integrals of order
are, respectively, the left and right Riemann-Liouville
fractional integrals of order
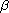 ,
,
![$F: [0,T]\times\mathbb{R}^N\to\mathbb{R}$](gifs/ah.gif) is a given function.
Our interest in the above system arises from studying the steady fractional
advection dispersion equation.
By applying variational methods, we obtain sufficient conditions
under which the above equation has at least three solutions.
Our results are new even for the special case when
is a given function.
Our interest in the above system arises from studying the steady fractional
advection dispersion equation.
By applying variational methods, we obtain sufficient conditions
under which the above equation has at least three solutions.
Our results are new even for the special case when
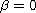 .
Examples are provided to illustrate the applicability of our results.
.
Examples are provided to illustrate the applicability of our results.
