Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 10, pp. 1-14.
Nonlinear convection in reaction-diffusion equations under
dynamical boundary conditions
Gaelle Pincet Mailly, Jean-Francois Rault
Abstract:
We study the blow-up phenomena for positive solutions of nonlinear
reaction-diffusion equations including a nonlinear convection term
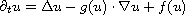 in a bounded
domain of
in a bounded
domain of
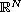 under the dissipative dynamical boundary
conditions
under the dissipative dynamical boundary
conditions
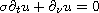 .
Some conditions on g and f are discussed to state if the positive
solutions blow up in finite time or not. Moreover, for certain
classes of nonlinearities, an upper-bound for the blow-up time
can be derived and the blow-up rate can be determined.
.
Some conditions on g and f are discussed to state if the positive
solutions blow up in finite time or not. Moreover, for certain
classes of nonlinearities, an upper-bound for the blow-up time
can be derived and the blow-up rate can be determined.
Submitted July 10, 2012. Published January 9, 2013.
Math Subject Classifications: 35K55, 35B44.
Key Words: Nonlinear parabolic problem; dynamical boundary conditions;
lower and upper-solution; blow-up; global solution.
Show me the PDF file (275 KB),
TEX file, and other files for this article.
 |
Gaëlle Pincet Mailly
LMPA Joseph Liouville FR 2956 CNRS
Université Lille Nord de France
50 rue F. Buisson, B. P. 699, F-62228 Calais Cedex, France
email: mailly@lmpa.univ-littoral.fr
|
|---|
 |
Jean-Fran&ccdil;ois Rault
LMPA Joseph Liouville FR 2956 CNRS
Université Lille Nord de France
50 rue F. Buisson, B. P. 699, F-62228 Calais Cedex, France
email: jfrault@lmpa.univ-littoral.fr
|
|---|
Return to the EJDE web page
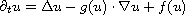 in a bounded
domain of
in a bounded
domain of
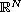 under the dissipative dynamical boundary
conditions
under the dissipative dynamical boundary
conditions
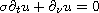 .
Some conditions on g and f are discussed to state if the positive
solutions blow up in finite time or not. Moreover, for certain
classes of nonlinearities, an upper-bound for the blow-up time
can be derived and the blow-up rate can be determined.
.
Some conditions on g and f are discussed to state if the positive
solutions blow up in finite time or not. Moreover, for certain
classes of nonlinearities, an upper-bound for the blow-up time
can be derived and the blow-up rate can be determined.

