Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 08, pp. 1-10.
Existence and uniqueness of anti-periodic solutions
for nonlinear third-order differential inclusions
Touma Haddad, Tahar Haddad
Abstract:
In this article, we study the existence of anti-periodic
solutions for the third-order differential inclusion
![$$\displaylines{
u'''(t)\in \partial\varphi(u'(t))+F(t,u(t))\quad \hbox{a.e. on }[0,T]\cr
u(0)=-u(T), \quad u'(0)=-u'(T),\quad u''(0)=-u''(T),
}$$](gifs/aa.gif)
where
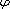 is a proper convex, lower semicontinuous and even
function, and F is an upper semicontinuous convex compact
set-valued mapping. Also uniqueness of anti-periodic
solution is studied.
is a proper convex, lower semicontinuous and even
function, and F is an upper semicontinuous convex compact
set-valued mapping. Also uniqueness of anti-periodic
solution is studied.
Submitted September 28, 2012. Published January 09, 2013.
Math Subject Classifications: 34C25, 34G20, 49J52.
Key Words: Anti-periodic solution; differential inclusions; subdifferential.
Show me the PDF file (212 KB),
TEX file, and other files for this article.
 |
Touma Haddad
Département de Mathématiques,
Faculté des Sciences
Université de Jijel, B.P. 98, Algérie
email: touma.haddad@yahoo.com
|
|---|
 |
Tahar Haddad
Laboratoire LMPA,
Faculté des Sciences
Université de Jijel, B.P. 98, Algérie
email: haddadtr2000@yahoo.fr
|
|---|
Return to the EJDE web page
![$$\displaylines{
u'''(t)\in \partial\varphi(u'(t))+F(t,u(t))\quad \hbox{a.e. on }[0,T]\cr
u(0)=-u(T), \quad u'(0)=-u'(T),\quad u''(0)=-u''(T),
}$$](gifs/aa.gif)
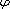 is a proper convex, lower semicontinuous and even
function, and F is an upper semicontinuous convex compact
set-valued mapping. Also uniqueness of anti-periodic
solution is studied.
is a proper convex, lower semicontinuous and even
function, and F is an upper semicontinuous convex compact
set-valued mapping. Also uniqueness of anti-periodic
solution is studied.

