Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 05, pp. 1-11.
Existence of solutions for critical Henon equations in hyperbolic spaces
Haiyang He, Jing Qiu
Abstract:
In this article, we use variational methods to prove that for a
suitable value of
 , the problem
, the problem
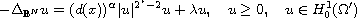
possesses at least one non-trivial solution u as
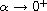 ,
where
,
where
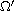 is a bounded domain in Hyperbolic space
is a bounded domain in Hyperbolic space
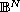 ,
,
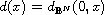 .
.
 denotes
the Laplace-Beltrami operator on
denotes
the Laplace-Beltrami operator on
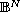 ,
,
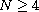 ,
,
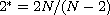 .
.
Submitted June 13, 2012. Published January 8, 2013.
Math Subject Classifications: 58J05, 35J60.
Key Words: Henon equations; mountain pass theorem;
critical growth; hyperbolic space.
Show me the PDF file (239 KB),
TEX file, and other files for this article.
 |
Haiyang He
College of Mathematics and Computer Science
Key Laboratory of High Performance Computing
and Stochastic Information Processing
Hunan Normal University, Changsha, Hunan 410081, China
email: hehy917@yahoo.com.cn
|
|---|
 |
Jing Qiu
College of Mathematics and Computer Science
Key Laboratory of High Performance Computing
and Stochastic Information Processing
Hunan Normal University, Changsha, Hunan 410081, China
email: qiujing0626@163.com
|
|---|
Return to the EJDE web page
 , the problem
, the problem
 ,
where
,
where
 is a bounded domain in Hyperbolic space
is a bounded domain in Hyperbolic space
 ,
,
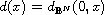 .
.
 denotes
the Laplace-Beltrami operator on
denotes
the Laplace-Beltrami operator on
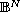 ,
,
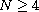 ,
,
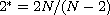 .
.

