Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 98, pp. 1-22.
Nonlinear fractional differential equations and inclusions
of arbitrary order and multi-strip boundary conditions
Bashir Ahmad, Sotiris K. Ntouyas
Abstract:
We study boundary value problems of nonlinear fractional
differential equations and inclusions of order
![$q \in (m-1, m]$](gifs/aa.gif) ,
,
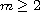 with multi-strip boundary conditions. Multi-strip boundary
conditions may be regarded as the generalization of multi-point
boundary conditions. Our problem is new in the sense
that we consider a nonlocal strip condition of the form:
with multi-strip boundary conditions. Multi-strip boundary
conditions may be regarded as the generalization of multi-point
boundary conditions. Our problem is new in the sense
that we consider a nonlocal strip condition of the form:
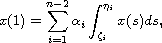
which can be viewed as an extension of a multi-point nonlocal
boundary condition:
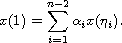
In fact, the strip condition corresponds to a continuous distribution
of the values of the unknown function on arbitrary finite
segments
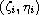 of the interval
of the interval
![$[0,1]$](gifs/af.gif) and the effect
of these strips is accumulated at
and the effect
of these strips is accumulated at
 .
Such problems occur in
the applied fields such as wave propagation and geophysics. Some
new existence and uniqueness results are obtained by using a
variety of fixed point theorems. Some illustrative examples are
also discussed.
.
Such problems occur in
the applied fields such as wave propagation and geophysics. Some
new existence and uniqueness results are obtained by using a
variety of fixed point theorems. Some illustrative examples are
also discussed.
Submitted May 20, 2012. Published June 12, 2012.
Math Subject Classifications: 26A33, 34A60, 34B10, 34B15.
Key Words: Fractional differential inclusions; integral boundary conditions;
existence; contraction principle; Krasnoselskii's fixed point theorem;
Leray-Schauder degree; Leray-Schauder nonlinear alternative;
nonlinear contractions.
Show me the PDF file (337 KB),
TEX file, and other files for this article.
 |
Bashir Ahmad
Department of Mathematics, Faculty of Science
King Abdulaziz University
P.O. Box 80203, Jeddah 21589, Saudi Arabia
email: bashir_qau@yahoo.com
|
|---|
 |
Sotiris K. Ntouyas
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: sntouyas@uoi.gr
|
Return to the EJDE web page
![$q \in (m-1, m]$](gifs/aa.gif) ,
,
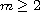 with multi-strip boundary conditions. Multi-strip boundary
conditions may be regarded as the generalization of multi-point
boundary conditions. Our problem is new in the sense
that we consider a nonlocal strip condition of the form:
with multi-strip boundary conditions. Multi-strip boundary
conditions may be regarded as the generalization of multi-point
boundary conditions. Our problem is new in the sense
that we consider a nonlocal strip condition of the form:
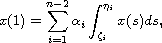
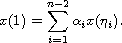
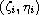 of the interval
of the interval
![$[0,1]$](gifs/af.gif) and the effect
of these strips is accumulated at
and the effect
of these strips is accumulated at
 .
Such problems occur in
the applied fields such as wave propagation and geophysics. Some
new existence and uniqueness results are obtained by using a
variety of fixed point theorems. Some illustrative examples are
also discussed.
.
Such problems occur in
the applied fields such as wave propagation and geophysics. Some
new existence and uniqueness results are obtained by using a
variety of fixed point theorems. Some illustrative examples are
also discussed.

