Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 83, pp. 1-7.
Solutions to over-determined systems of partial differential equations
related to Hamiltonian stationary Lagrangian surfaces
Bang-Yen Chen
Abstract:
This article concerns the over-determined system of partial
differential equations
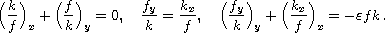
It was shown in [6, Theorem 8.1] that this system
with
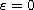 admits traveling wave solutions as well as
non-traveling wave solutions.
In this article we solve completely this system when
admits traveling wave solutions as well as
non-traveling wave solutions.
In this article we solve completely this system when
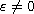 .
Our main result states that this system admits only traveling wave
solutions, whenever
.
Our main result states that this system admits only traveling wave
solutions, whenever
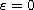 .
.
Submitted December 1, 2011. Published May 23, 2012.
Math Subject Classifications: 35N05, 35C07, 35C99.
Key Words: Over-determined PDE system; traveling wave solution;
exact solution; Hamiltonian stationary Lagrangian surfaces.
Show me the PDF file (212 KB),
TEX file, and other files for this article.
 |
Bang-Yen Chen
Department of Mathematics,
Michigan State University
619 Red Cedar Road
East Lansing, Michigan 48824-1027, USA
email: bychen@math.msu.edu
|
|---|
Return to the EJDE web page
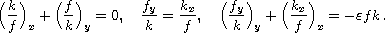
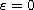 admits traveling wave solutions as well as
non-traveling wave solutions.
In this article we solve completely this system when
admits traveling wave solutions as well as
non-traveling wave solutions.
In this article we solve completely this system when
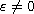 .
Our main result states that this system admits only traveling wave
solutions, whenever
.
Our main result states that this system admits only traveling wave
solutions, whenever
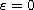 .
.
