Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 79, pp. 1-20.
Strongly nonlinear nonhomogeneous elliptic unilateral problems
with L^1 data and no sign conditions
Elhoussine Azroul, Hicham Redwane, Chihab Yazough
Abstract:
In this article, we prove the existence of solutions to unilateral
problems involving nonlinear operators of the form:
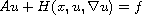
where
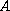 is a Leray Lions operator from
is a Leray Lions operator from
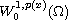 into its dual
into its dual
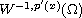 and
and
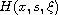 is the nonlinear term satisfying some growth condition
but no sign condition. The right hand side
is the nonlinear term satisfying some growth condition
but no sign condition. The right hand side
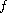 belong to
belong to
 .
.
Submitted September 19, 2011. Published May 15, 2012.
Math Subject Classifications: 35J60.
Key Words: Entropy solutions; variable exponent; unilateral problem.
Show me the PDF file (313 KB),
TEX file, and other files for this article.
 |
Elhoussine Azroul
University of Fez, Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics
B.P. 1796 Atlas Fez, Morocco
email: azroul_elhoussine@yahoo.fr
|
|---|
 |
Hicham Redwane
Faculté des Sciences Juridiques, Economiques et Sociales
University Hassan 1
B.P. 784, Settat, Morocco
email: redwane_hicham@yahoo.fr
|
|---|
 |
Chihab Yazough
University of Fez, Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics
B.P. 1796 Atlas Fez, Morocco
email: chihabyazough@gmail.com
|
|---|
Return to the EJDE web page
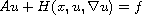
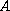 is a Leray Lions operator from
is a Leray Lions operator from
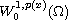 into its dual
into its dual
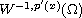 and
and
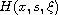 is the nonlinear term satisfying some growth condition
but no sign condition. The right hand side
is the nonlinear term satisfying some growth condition
but no sign condition. The right hand side
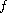 belong to
belong to
 .
.


