Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 63, pp. 1-14.
Existence of positive solutions for singular fractional
differential equations with integral boundary conditions
Jingfu Jin, Xiping Liu, Mei Jia
Abstract:
This article shows the existence of a positive solution
for the singular fractional differential equation with integral
boundary condition
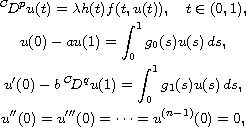
where
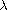 is a parameter and the nonlinear term is allowed to
be singular at t=0, 1 and u=0.
We obtain an explicit interval for
is a parameter and the nonlinear term is allowed to
be singular at t=0, 1 and u=0.
We obtain an explicit interval for
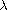 such that for any
such that for any
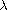 in
this interval, existence of at least one positive solution is guaranteed.
Our approach is by a fixed point theory in cones combined with linear
operator theory.
in
this interval, existence of at least one positive solution is guaranteed.
Our approach is by a fixed point theory in cones combined with linear
operator theory.
Submitted January 17, 2012. Published April 19, 2012.
Math Subject Classifications: 34B16, 34B18, 26A33
Key Words: Caputo derivative; fractional differential equations;
positive solutions; integral boundary conditions;
singular differential equation
Show me the PDF file (246 KB),
TEX file, and other files for this article.
 |
Jingfu Jin
College of Science
University of Shanghai for Science and Technology
Shanghai 200093, China
email: jinjingfu2005@126.com
|
|---|
 |
Xiping Liu
College of Science
University of Shanghai for Science and Technology
Shanghai 200093, China
email: xipingliu@163.com
|
|---|
 |
Mei Jia
College of Science
University of Shanghai for Science and Technology
Shanghai 200093, China
email: jiamei-usst@163.com
|
|---|
Return to the EJDE web page
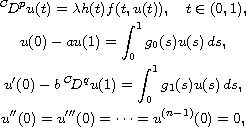
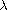 is a parameter and the nonlinear term is allowed to
be singular at t=0, 1 and u=0.
We obtain an explicit interval for
is a parameter and the nonlinear term is allowed to
be singular at t=0, 1 and u=0.
We obtain an explicit interval for
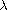 such that for any
such that for any
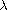 in
this interval, existence of at least one positive solution is guaranteed.
Our approach is by a fixed point theory in cones combined with linear
operator theory.
in
this interval, existence of at least one positive solution is guaranteed.
Our approach is by a fixed point theory in cones combined with linear
operator theory.


