Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 57, pp. 1-14.
Periodic solutions for neutral functional differential equations
with impulses on time scales
Yongkun Li, Xiaoyan Dou, Jianwen Zhou
Abstract:
Let
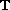 be a periodic time scale. We use Krasnoselskii's
fixed point theorem to show that the neutral functional differential
equation with impulses
be a periodic time scale. We use Krasnoselskii's
fixed point theorem to show that the neutral functional differential
equation with impulses
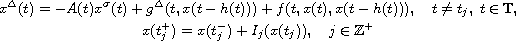
has a periodic solution. Under a slightly more stringent conditions
we show that the periodic solution is unique using the contraction
mapping principle.
Submitted August 22, 2011 Published April 10, 2012.
Math Subject Classifications: 34N05, 34K13, 34K40, 34K45.
Key Words: Positive periodic solution; neutral functional differential
equations; impulses; Krasnoselskii fixed point; time scales.
Show me the PDF file (248 KB),
TEX file, and other files for this article.
 |
Yongkun Li
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email: yklie@ynu.edu.cn
|
|---|
 |
Xiaoyan Dou
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email: douxy21@163.com
|
|---|
 |
Jianwen Zhou
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email: zhoujianwen2007@126.com
|
|---|
Return to the EJDE web page
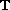 be a periodic time scale. We use Krasnoselskii's
fixed point theorem to show that the neutral functional differential
equation with impulses
be a periodic time scale. We use Krasnoselskii's
fixed point theorem to show that the neutral functional differential
equation with impulses