Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 56, pp. 1-16.
Existence and topological structure of solution sets for
phi-Laplacian impulsive differential equations
Johnny Henderson, Abdelghani Ouahab, Samia Youcefi
Abstract:
In this article, we present results on the existence and the topological structure
of the solution set for initial-value problems for the first-order
impulsive differential equation
![$$\displaylines{
(\phi(y'))' = f(t,y(t)), \quad\hbox{a.e. } t\in [0,b],\cr
y(t^+_{k})-y(t^-_k)=I_{k}(y(t_{k}^{-})), \quad k=1,\dots,m,\cr
y'(t^+_{k})-y'(t^-_k)=\bar I_{k}(y'(t_{k}^{-})), \quad k=1,\dots,m,\cr
y(0)=A,\quad y'(0)=B,
}$$](gifs/aa.gif)
where
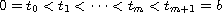 ,
,
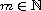 .
The functions
.
The functions
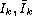 characterize the jump in the
solutions at impulse points
characterize the jump in the
solutions at impulse points
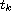 ,
,
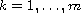 .
For the final result of the paper, the hypotheses are modified so
that the nonlinearity
.
For the final result of the paper, the hypotheses are modified so
that the nonlinearity
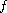 depends on
depends on
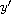 ,
but the impulsive conditions
and initial conditions remain the same.
,
but the impulsive conditions
and initial conditions remain the same.
Submitted January 20, 2012. Published April 6, 2012.
Math Subject Classifications: 34A37, 34K45.
Key Words: phi-Laplacian; fixed point theorems; impulsive solution;
compactness.
Show me the PDF file (263 KB),
TEX file, and other files for this article.
 |
Johnny Henderson
Department of Mathematics, Baylor University
Waco, TX 76798-7328, USA
email: Johnny_Henderson@baylor.edu
|
|---|
 |
Abdelghani Ouahab
Laboratory of Mathematics, Sidi-Bel-Abbès University
PoBox 89, 22000 Sidi-Bel-Abbès, Algeria
email: agh_ouahab@yahoo.fr
|
|---|
| |
Samia Youcefi
Laboratory of Mathematics, Sidi-Bel-Abbès University
PoBox 89, 22000 Sidi-Bel-Abbès, Algeria
email: youcefi.samia@yahoo.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
(\phi(y'))' = f(t,y(t)), \quad\hbox{a.e. } t\in [0,b],\cr
y(t^+_{k})-y(t^-_k)=I_{k}(y(t_{k}^{-})), \quad k=1,\dots,m,\cr
y'(t^+_{k})-y'(t^-_k)=\bar I_{k}(y'(t_{k}^{-})), \quad k=1,\dots,m,\cr
y(0)=A,\quad y'(0)=B,
}$$](gifs/aa.gif)
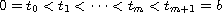 ,
,
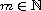 .
The functions
.
The functions
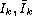 characterize the jump in the
solutions at impulse points
characterize the jump in the
solutions at impulse points
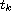 ,
,
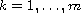 .
For the final result of the paper, the hypotheses are modified so
that the nonlinearity
.
For the final result of the paper, the hypotheses are modified so
that the nonlinearity
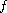 depends on
depends on
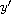 ,
but the impulsive conditions
and initial conditions remain the same.
,
but the impulsive conditions
and initial conditions remain the same.

