Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 54, pp. 1-10.
Existence of solutions for multi-point nonlinear differential
equations of fractional orders with integral boundary conditions
Gang Wang, Wenbin Liu, Can Ren
Abstract:
In this article, we study the multi-point boundary-value problem
of nonlinear fractional differential equation
![$$\displaylines{
D^\alpha_{0+}u(t)=f(t,u(t)),\quad 1<\alpha\leq 2,\; t\in[0,T],\; T>0,\cr
I_{0+}^{2-\alpha}u(t)|_{t=0}=0,\quad
D_{0+}^{\alpha-2}u(T)=\sum_{i=1}^ma_i I_{0+}^{\alpha-1}u(\xi_i),
}$$](gifs/aa.gif)
where
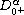 and
and
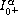 are the standard Riemann-Liouville
fractional derivative and fractional integral respectively.
Some existence and uniqueness results are obtained by applying some standard
fixed point principles. Several examples are given to illustrate the results.
are the standard Riemann-Liouville
fractional derivative and fractional integral respectively.
Some existence and uniqueness results are obtained by applying some standard
fixed point principles. Several examples are given to illustrate the results.
Submitted November 27, 2011. Published April 5, 2012.
Math Subject Classifications: 34B15.
Key Words: Fractional differential equation; boundary value problem;
fixed point theorem; existence and uniqueness.
Show me the PDF file (230 KB),
TEX file, and other files for this article.
 |
Gang Wang
Department of mathematics
University of Mining and Technology
Xuzhou 221008, China
email: wangg0824@163.com
|
|---|
 |
Wenbin Liu
Department of mathematics
University of Mining and Technology
Xuzhou 221008, China
email: wblium@163.com
|
|---|
 |
Can Ren
Department of mathematics
University of Mining and Technology
Xuzhou 221008, China
email: rencan0502@163.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
D^\alpha_{0+}u(t)=f(t,u(t)),\quad 1<\alpha\leq 2,\; t\in[0,T],\; T>0,\cr
I_{0+}^{2-\alpha}u(t)|_{t=0}=0,\quad
D_{0+}^{\alpha-2}u(T)=\sum_{i=1}^ma_i I_{0+}^{\alpha-1}u(\xi_i),
}$$](gifs/aa.gif)
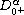 and
and
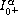 are the standard Riemann-Liouville
fractional derivative and fractional integral respectively.
Some existence and uniqueness results are obtained by applying some standard
fixed point principles. Several examples are given to illustrate the results.
are the standard Riemann-Liouville
fractional derivative and fractional integral respectively.
Some existence and uniqueness results are obtained by applying some standard
fixed point principles. Several examples are given to illustrate the results.


