Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 51, pp. 1-14.
Existence and uniform asymptotic stability for an abstract differential equation
with infinite delay
Cung The Anh, Le Van Hieu
Abstract:
Using the Contraction Mapping Principle, we study the existence, uniqueness,
and uniform asymptotic stability of solutions to an abstract differential
equation with infinite delay of the form
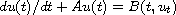 ,
where A is a positive sectorial operator and the nonlinear part B
is Lipschitz continuous with respect to a fractional power of A in the
second variable and the Lipschitz coefficient may depend on time t.
Some special cases and examples are provided to illustrate the results
obtained.
,
where A is a positive sectorial operator and the nonlinear part B
is Lipschitz continuous with respect to a fractional power of A in the
second variable and the Lipschitz coefficient may depend on time t.
Some special cases and examples are provided to illustrate the results
obtained.
Submitted June 3, 2011. Published March 29, 2012.
Math Subject Classifications: 35B35, 37L15.
Key Words: Infinite delay; sectorial operator; mild solution;
uniform asymptotic stability; fixed point method.
Show me the PDF file (254 KB),
TEX file, and other files for this article.
 |
Cung The Anh
Department of Mathematics
Hanoi National University of Education
136 Xuan Thuy, Cau Giay, Hanoi, Vietnam
email: anhctmath@hnue.edu.vn
|
|---|
 |
Le Van Hieu
Academy of Journalism and Communication
36 Xuan Thuy, Cau Giay, Hanoi, Vietnam
email: hieulv@ajc.edu.vn
|
|---|
Return to the EJDE web page
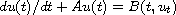 ,
where A is a positive sectorial operator and the nonlinear part B
is Lipschitz continuous with respect to a fractional power of A in the
second variable and the Lipschitz coefficient may depend on time t.
Some special cases and examples are provided to illustrate the results
obtained.
,
where A is a positive sectorial operator and the nonlinear part B
is Lipschitz continuous with respect to a fractional power of A in the
second variable and the Lipschitz coefficient may depend on time t.
Some special cases and examples are provided to illustrate the results
obtained.

