In this article, we prove the existence of a weak solution for the degenerate semilinear elliptic Dirichlet boundary-value problem
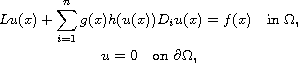
in a suitable weighted Sobolev space. Here
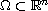 ,
,
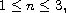 is not necessarily bounded.
is not necessarily bounded.
Rasmita Kar
Abstract:
In this article, we prove the existence of a weak solution for the
degenerate semilinear elliptic Dirichlet boundary-value problem
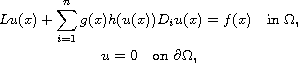
in a suitable weighted Sobolev space. Here
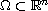 ,
,
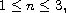 is not necessarily bounded.
is not necessarily bounded.
Submitted September 17, 2011. Published March 20, 2012.
Math Subject Classifications: 46E35, 35J61
Key Words: Semilinear elliptic boundary value problem; unbounded domain;
pseudomonotone operator.
Show me the PDF file (241 KB), TEX file, and other files for this article.
 |
Rasmita Kar Department of Mathematics and Statistics Indian Institute of Technology Kanpur, 208016 India email: rasmi07@gmail.com |
|---|
Return to the EJDE web page