In this article we study the existence of solutions to eigenvalue problem
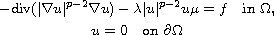
where
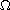 is a bounded domain in
is a bounded domain in
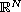 and
and
 is a
nonnegative Radon measure.
is a
nonnegative Radon measure.
Nedra Belhaj Rhouma, Wahid Sayeb
Abstract:
In this article we study the existence of solutions to eigenvalue problem
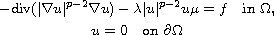
where
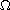 is a bounded domain in
is a bounded domain in
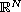 and
and
 is a
nonnegative Radon measure.
is a
nonnegative Radon measure.
Submitted June 11, 2011. Published February 29, 2012.
Math Subject Classifications: 34B15, 34B18, 35A01, 35A02.
Key Words: Dirichlet problem; p-Laplacian; genus function; eigenfunction;
nonlinear eigenvalue problem; Palais-Smale condition;
mountain-pass theorem; critical point.
Show me the PDF file (302 KB), TEX file, and other files for this article.
 |
Nedra Belhaj Rhouma Departement de Mathématiques, Facultédes sciences de Tunis Université Tunis El Manar Campus Universitaire 2092, Tunis, Tunisia email: nedra.belhajrhouma@fst.rnu.tn |
|---|---|
 |
Wahid Sayeb Departement de Mathématiques, Facultédes sciences de Tunis Université Tunis El Manar Campus Universitaire 2092, Tunis, Tunisia email: wahid.sayeb@yahoo.fr |
Return to the EJDE web page