Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 30, pp. 1-13.
Higher order viability problem in Banach spaces
Myelkebir Aitalioubrahim, Said Sajid
Abstract:
We show the existence of viable solutions to the differential inclusion
![$$\displaylines{
x^{(k)}(t) \in F(t,x(t))\cr
x(0)=x_{0},\quad x^{(i)}(0)=y^i_{0},\quad i=1,\dots,k-1,\cr
x(t) \in K\quad\hbox{on } [0,T],
}$$](gifs/aa.gif)
where
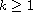 , K is a closed subset of a separable Banach space
and F(t,x) is an integrable bounded multifunction with closed values,
(strongly) measurable in t and Lipschitz continuous in x.
, K is a closed subset of a separable Banach space
and F(t,x) is an integrable bounded multifunction with closed values,
(strongly) measurable in t and Lipschitz continuous in x.
Submitted May 30, 2011. Published February 21, 2012.
Math Subject Classifications: 34A60.
Key Words: Differential inclusion; measurability; selection; viability.
Show me the PDF file (232 KB),
TEX file, and other files for this article.
 |
Myelkebir Aitalioubrahim
University Hassan II-Mohammedia
Laboratory Mathematics, Cryptography and Mecanics
F.S.T, BP 146, Mohammedia, Morocco
email: aitalifr@yahoo.fr
|
|---|
 |
Said Sajid
University Hassan II-Mohammedia
Laboratory Mathematics, Cryptography and Mecanics
F.S.T, BP 146, Mohammedia, Morocco
email: saidsajid@hotmail.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
x^{(k)}(t) \in F(t,x(t))\cr
x(0)=x_{0},\quad x^{(i)}(0)=y^i_{0},\quad i=1,\dots,k-1,\cr
x(t) \in K\quad\hbox{on } [0,T],
}$$](gifs/aa.gif)
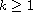 , K is a closed subset of a separable Banach space
and F(t,x) is an integrable bounded multifunction with closed values,
(strongly) measurable in t and Lipschitz continuous in x.
, K is a closed subset of a separable Banach space
and F(t,x) is an integrable bounded multifunction with closed values,
(strongly) measurable in t and Lipschitz continuous in x.

