Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 29, pp. 1-9.
Oscillation of solutions to third-order half-linear neutral
differential equations
Jozef Dzurina, Ethiraju Thandapani, Sivaraj Tamilvanan
Abstract:
In this article, we study the oscillation of solutions to the
third-order neutral differential equations
![$$
\Big(a(t)\big([x(t)\pm p(t)x(\delta(t))]''\big)^\alpha\Big)' +
q(t)x^\alpha(\tau(t)) = 0.
$$](gifs/aa.gif)
Sufficient conditions are established so that every
solution is either oscillatory or converges to zero.
In particular, we extend the results obtain in [1] for
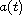 non-decreasing, to the non-increasing case.
non-decreasing, to the non-increasing case.
Submitted November 12, 2011. Published February 21, 2012.
Math Subject Classifications: 34K11, 34C10.
Key Words: Third-order neutral differential equation;
Riccati transformation; oscillation of solutions.
Show me the PDF file (216 KB),
TEX file, and other files for this article.
 |
Jozef Dzurina
Department of Mathematics
Faculty of Electrical Engineering and Informatics
Technical University of Kosice
Letna 9, 042 00 Kosice, Slovakia
email: jozef.dzurina@tuke.sk
|
|---|
 |
Ethiraju Thandapani
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai, 600 005, India
email: ethandapani@yahoo.co.in
|
|---|
 |
Sivaraj Tamilvanan
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai, 600 005, India
email: saitamilvanan@yahoo.in
|
|---|
Return to the EJDE web page
![$$
\Big(a(t)\big([x(t)\pm p(t)x(\delta(t))]''\big)^\alpha\Big)' +
q(t)x^\alpha(\tau(t)) = 0.
$$](gifs/aa.gif)
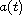 non-decreasing, to the non-increasing case.
non-decreasing, to the non-increasing case.


