Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 234, pp. 1-11.
Existence and uniqueness of positive solutions to higher-order
nonlinear fractional differential equation with integral
boundary conditions
Chenxing Zhou
Abstract:
In this article, we consider the nonlinear fractional order
three-point boundary-value problem
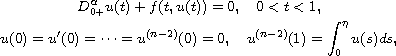
where
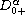 is the standard Riemann-Liouville fractional
derivative,
is the standard Riemann-Liouville fractional
derivative,
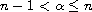 ,
,
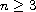 . By using a fixed-point
theorem in partially ordered sets, we obtain sufficient conditions
for the existence and uniqueness of positive and nondecreasing
solutions to the above boundary value problem.
. By using a fixed-point
theorem in partially ordered sets, we obtain sufficient conditions
for the existence and uniqueness of positive and nondecreasing
solutions to the above boundary value problem.
Submitted September 19, 2012. Published December 21, 2012.
Math Subject Classifications: 26A33, 34B18, 34B27.
Key Words: Partially ordered sets; fixed-point theorem; positive solution.
Show me the PDF file (224 KB),
TEX file, and other files for this article.
 |
Chenxing Zhou
College of Mathematics
Changchun Normal University
Changchun 130032, Jilin, China
|
|---|
Return to the EJDE web page
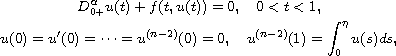
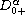 is the standard Riemann-Liouville fractional
derivative,
is the standard Riemann-Liouville fractional
derivative,
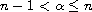 ,
,
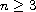 . By using a fixed-point
theorem in partially ordered sets, we obtain sufficient conditions
for the existence and uniqueness of positive and nondecreasing
solutions to the above boundary value problem.
. By using a fixed-point
theorem in partially ordered sets, we obtain sufficient conditions
for the existence and uniqueness of positive and nondecreasing
solutions to the above boundary value problem.
