Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 232, pp. 1-8.
Anti-periodic solutions to Rayleigh-type equations with
two deviating arguments
Meiqiang Feng, Xuemei Zhang
Abstract:
In this article, the Rayleigh equation with two deviating arguments
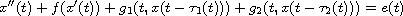
is studied. By using Leray-Schauder fixed point theorem, we obtain
the existence of anti-periodic solutions to this equation.
The results are illustrated with an example, which can not be
handled using previous results.
Submitted September 20, 2012. Published December 21, 2012.
Math Subject Classifications: 34K13, 34K15, 34C25.
Key Words: Rayleigh equation; anti-periodic solution; deviating argument.
Show me the PDF file (207 KB),
TEX file, and other files for this article.
 |
Meiqiang Feng
School of Applied Science
Beijing Information Science and Technology University
Beijing, 100192, China
email: meiqiangfeng@sina.com
|
|---|
 |
Xuemei Zhang
Department of Mathematics and Physics
North China Electric Power University
Beijing, 102206, China
email: zxm74@sina.com
|
|---|
Return to the EJDE web page