In the previous article [Y.-X. Wang and W.-T. Li, J. Differential Equations, 251 (2011) 1670-1695], the authors have shown that the set of positive stationary solutions of a cross-diffusive Lotka-Volterra cooperative system can form an unbounded fish-hook shaped branch
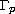 .
In the present paper,
we will show some criteria for the stability of positive stationary
solutions on
.
In the present paper,
we will show some criteria for the stability of positive stationary
solutions on
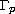 .
Our results assert that if
.
Our results assert that if
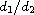 is
small enough, then unstable positive stationary solutions bifurcate
from semitrivial solutions, the stability changes only at every
turning point of
is
small enough, then unstable positive stationary solutions bifurcate
from semitrivial solutions, the stability changes only at every
turning point of
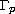 and no Hopf bifurcation occurs. While as
and no Hopf bifurcation occurs. While as
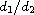 becomes large, the stability has a drastic change when
becomes large, the stability has a drastic change when
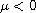 in the supercritical case. Original stable positive
stationary solutions at certain point may lose their stability, and
Hopf bifurcation can occur. These results are very different from
those of the spatially homogeneous case.
in the supercritical case. Original stable positive
stationary solutions at certain point may lose their stability, and
Hopf bifurcation can occur. These results are very different from
those of the spatially homogeneous case.


