Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 215, pp. 1-27.
Positive solutions of fractional differential
equations with derivative terms
Cuiping Cheng, Zhaosheng Feng, Youhui Su
Abstract:
In this article, we are concerned with the existence of positive
solutions for nonlinear fractional differential equation
whose nonlinearity contains the first-order derivative,
![$$\displaylines{
D_{0^+}^{\alpha}u(t)+f(t,u(t),u'(t))=0,\quad t\in (0,1),\;
n-1<\alpha\leq n,\cr
u^{(i)}(0)=0, \quad i=0,1,2,\dots,n-2,\cr
[D_{0^+}^{\beta}u(t)]_{t=1}=0, \quad 2\leq\beta\leq n-2,
}$$](gifs/aa.gif)
where
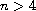
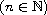 ,
,
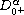 is the
standard Riemann-Liouville fractional derivative of order
is the
standard Riemann-Liouville fractional derivative of order
 and
and
![$f(t,u,u'):[0,1] \times [0,\infty)\times(-\infty,+\infty)
\to [0,\infty)$](gifs/af.gif) satisfies the Caratheodory type condition.
Sufficient conditions are obtained for the existence of
at least one or two positive solutions by using the nonlinear
alternative of the Leray-Schauder type and Krasnosel'skii's fixed
point theorem. In addition, several other sufficient
conditions are established for the existence of at least triple,
n or 2n-1 positive solutions. Two examples
are given to illustrate our theoretical results.
satisfies the Caratheodory type condition.
Sufficient conditions are obtained for the existence of
at least one or two positive solutions by using the nonlinear
alternative of the Leray-Schauder type and Krasnosel'skii's fixed
point theorem. In addition, several other sufficient
conditions are established for the existence of at least triple,
n or 2n-1 positive solutions. Two examples
are given to illustrate our theoretical results.
Submitted August 15, 2012. Published November 29, 2012.
Math Subject Classifications: 34A08, 34B18, 34K37.
Key Words: Positive solution; equicontinuity;
fractional differential equation; fixed point theorem;
Caratheodory type condition.
Show me the PDF file (350 KB),
TEX file, and other files for this article.
 |
Cuiping Cheng
Department of Applied Mathematics
Hangzhou Dianzi University
Hangzhou 310018, China
email: chengcp0611@163.com
|
|---|
 |
Zhaosheng Feng
Department of Mathematics
University of Texas-Pan American
Edinburg, TX 78539, USA
email: zsfeng@utpa.edu; fax: (956) 665-5091
|
|---|
 |
Youhui Su
Department of Mathematics
Xuzhou Institute of Technology, Xuzhou 221116, China
Department of Mathematics, Indiana University
Bloomington, IN 47405, USA
email: youhsu@indiana.edu
|
|---|
Return to the EJDE web page
![$$\displaylines{
D_{0^+}^{\alpha}u(t)+f(t,u(t),u'(t))=0,\quad t\in (0,1),\;
n-1<\alpha\leq n,\cr
u^{(i)}(0)=0, \quad i=0,1,2,\dots,n-2,\cr
[D_{0^+}^{\beta}u(t)]_{t=1}=0, \quad 2\leq\beta\leq n-2,
}$$](gifs/aa.gif)
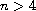
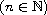 ,
,
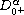 is the
standard Riemann-Liouville fractional derivative of order
is the
standard Riemann-Liouville fractional derivative of order
 and
and
![$f(t,u,u'):[0,1] \times [0,\infty)\times(-\infty,+\infty)
\to [0,\infty)$](gifs/af.gif) satisfies the Caratheodory type condition.
Sufficient conditions are obtained for the existence of
at least one or two positive solutions by using the nonlinear
alternative of the Leray-Schauder type and Krasnosel'skii's fixed
point theorem. In addition, several other sufficient
conditions are established for the existence of at least triple,
n or 2n-1 positive solutions. Two examples
are given to illustrate our theoretical results.
satisfies the Caratheodory type condition.
Sufficient conditions are obtained for the existence of
at least one or two positive solutions by using the nonlinear
alternative of the Leray-Schauder type and Krasnosel'skii's fixed
point theorem. In addition, several other sufficient
conditions are established for the existence of at least triple,
n or 2n-1 positive solutions. Two examples
are given to illustrate our theoretical results.


