We present a numerical scheme for the approximation of the system of partial differential equations of the Peaceman model for the miscible displacement of one fluid by another in a two dimensional porous medium. In this scheme, the velocity-pressure equations are treated by a mixed finite element discretization using the Raviart-Thomas element, and the concentration equation is approximated by a finite volume discretization using the Upstream scheme, knowing that the Raviart-Thomas element gives good approximations for fluids velocities and that the Upstream scheme is well suited for convection dominated equations. We prove a maximum principle for our approximate concentration more precisely
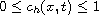 a.e. in
a.e. in
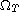 as long as some
grid conditions are satisfied - at the difference of
Chainais and Droniou [6]who have only observed that their
approximate concentration remains in
as long as some
grid conditions are satisfied - at the difference of
Chainais and Droniou [6]who have only observed that their
approximate concentration remains in
![$[0;1]$](gifs/ac.gif) (and such is the case
for other proposed numerical methods; e.g., [21,22].
Moreover our grid conditions are satisfied even with very large
time steps and spatial steps. Finally we prove the consistency
of the proposed scheme and thus are assured of convergence.
A numerical test is reported.
(and such is the case
for other proposed numerical methods; e.g., [21,22].
Moreover our grid conditions are satisfied even with very large
time steps and spatial steps. Finally we prove the consistency
of the proposed scheme and thus are assured of convergence.
A numerical test is reported.
