Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 180, pp. 1-7.
Analytic solutions for iterative functional differential equations
Pingping Zhang
Abstract:
Because of its technical difficulties the existence of analytic
solutions to the iterative differential equation
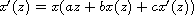 is a source of open problems.
In this article we obtain analytic solutions, using Schauder's fixed
point theorem. Also we present a unique solution which is a nonconstant
polynomial in the complex field.
is a source of open problems.
In this article we obtain analytic solutions, using Schauder's fixed
point theorem. Also we present a unique solution which is a nonconstant
polynomial in the complex field.
Submitted June 7, 2012. Published October 16, 2012.
Math Subject Classifications: 34K05, 39B12, 39B32.
Key Words: Iterative differential equation; existence;
analytic solution; polynomial solution.
Show me the PDF file (183 KB),
TEX file, and other files for this article.
 |
Pingping Zhang
Department of Mathematics, Sichuan University
Chengdu, Sichuan 610064, China
email: zhangpingpingmath@163.com
|
|---|
Return to the EJDE web page
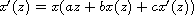 is a source of open problems.
In this article we obtain analytic solutions, using Schauder's fixed
point theorem. Also we present a unique solution which is a nonconstant
polynomial in the complex field.
is a source of open problems.
In this article we obtain analytic solutions, using Schauder's fixed
point theorem. Also we present a unique solution which is a nonconstant
polynomial in the complex field.
