Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 163, pp. 1-9.
Infinitely many solutions for class of
Navier boundary (p,q)-biharmonic systems
Mohammed Massar, El Miloud Hssini, Najib Tsouli
Abstract:
This article shows the existence and multiplicity of weak solutions
for the (p,q)-biharmonic type system
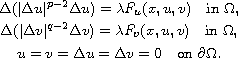
Under certain conditions on F, we show the existence of infinitely many weak
solutions. Our technical approach is based on Bonanno and Molica Bisci's
general critical point theorem.
Submitted June 4, 2012. Published September 21, 2012.
Math Subject Classifications: 35J40, 35J60.
Key Words: Navier value problem; infinitely many solutions;
Ricceri's variational principle.
Show me the PDF file (226 KB),
TEX file, and other files for this article.
 |
Mohammed Massar
University Mohamed I, Faculty of Sciences
Department of Mathematics, Oujda, Morocco
email: massarmed@hotmail.com
|
|---|
 |
El Miloud Hssini
University Mohamed I, Faculty of Sciences
Department of Mathematics, Oujda, Morocco
email: hssini1975@yahoo.fr
|
|---|
 |
Najib Tsouli
University Mohamed I, Faculty of Sciences
Department of Mathematics, Oujda, Morocco
email: tsouli@hotmail.com
|
|---|
Return to the EJDE web page