Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 162, pp. 1-14.
Nonexistence of asymptotically free solutions to nonlinear
Schrodinger systems
Nakao Hayashi, Chunhua Li, Pavel I. Naumkin
Abstract:
We consider the nonlinear Schrodinger systems
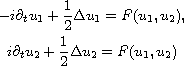
in n space dimensions, where F is a p-th order local or nonlocal
nonlinearity smooth up to order p, with
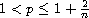 for
for
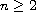 and
and
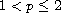 for n=1. These systems are related to higher
order nonlinear dispersive wave equations. We prove the non existence of
asymptotically free solutions in the critical and sub-critical cases.
for n=1. These systems are related to higher
order nonlinear dispersive wave equations. We prove the non existence of
asymptotically free solutions in the critical and sub-critical cases.
Submitted November 17, 2011. Published September 21, 2012.
Math Subject Classifications: 35Q55.
Key Words: Dispersive nonlinear waves; asymptotically free solutions.
Show me the PDF file (272 KB),
TEX file, and other files for this article.
 |
Nakao Hayashi
Department of Mathematics
Graduate School of Science, Osaka University
Osaka, Toyonaka, 560-0043, Japan
email: nhayashi@math.sci.osaka-u.ac.jp
|
|---|
 |
Chunhua Li
Department of Mathematics
Graduate School of Science, Yanbian University
Yanji City, Jilin Province, 133002, China
email: sxlch@ybu.edu.cn
|
|---|
 |
Pavel I. Naumkin
Centro de Ciencias Matemáticas
UNAM Campus Morelia, AP 61-3 (Xangari)
Morelia CP 58089, Michoacán, Mexico
email: pavelni@matmor.unam.mx
|
|---|
Return to the EJDE web page
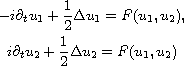
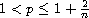 for
for
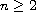 and
and
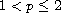 for n=1. These systems are related to higher
order nonlinear dispersive wave equations. We prove the non existence of
asymptotically free solutions in the critical and sub-critical cases.
for n=1. These systems are related to higher
order nonlinear dispersive wave equations. We prove the non existence of
asymptotically free solutions in the critical and sub-critical cases.


