Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 158, pp. 1-9.
Positive solutions for boundary-value problems with integral
boundary conditions on infinite intervals
Changlong Yu, Jufang Wang, Yanping Guo, Huixian Wei
Abstract:
In this article, we consider the existence of positive solutions
for a class of boundary value problems with integral boundary conditions
on infinite intervals
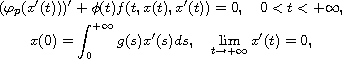
where
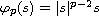 ,
,
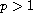 .
By applying the Avery-Peterson
fixed point theorem in a cone, we obtain the existence of three positive
solutions to the above boundary value problem and give an example at last.
.
By applying the Avery-Peterson
fixed point theorem in a cone, we obtain the existence of three positive
solutions to the above boundary value problem and give an example at last.
Submitted July 5, 2012. Published September 18, 2012.
Math Subject Classifications: 34B18, 34B15.
Key Words: Cone; Avery-Peterson fixed point theorem; positive solution;
integral boundary conditions; infinite interval.
Show me the PDF file (228 KB),
TEX file, and other files for this article.
 |
Changlong Yu
College of Sciences
Hebei University of Science and Technology
Shijiazhuang, 050018, China
email: changlongyu@126.com
|
|---|
| |
Jufang Wang
College of Sciences
Hebei University of Science and Technology
Shijiazhuang, 050018, China
email: wangjufang1981@126.com
|
|---|
| |
Yanping Guo
College of Sciences
Hebei University of Science and Technology
Shijiazhuang, 050018, China
|
|---|
| |
Huixian Wei
Department of Baise
Shijiazhuang Institute of Railway Technology
Shijiazhuang, 050041, China
|
|---|
Return to the EJDE web page
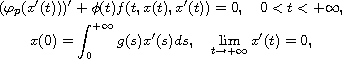
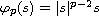 ,
,
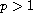 .
By applying the Avery-Peterson
fixed point theorem in a cone, we obtain the existence of three positive
solutions to the above boundary value problem and give an example at last.
.
By applying the Avery-Peterson
fixed point theorem in a cone, we obtain the existence of three positive
solutions to the above boundary value problem and give an example at last.
