Electron. J. Diff. Equ., Vol. 2012 (2012), No. 148, pp. 1-12.

Periodic solutions for p-Laplacian neutral functional differential equations with multiple deviating arguments

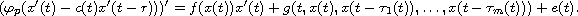
Aomar Anane, Omar Chakrone, Loubna Moutaouekkil

Abstract:
By means of Mawhin's continuation theorem, we prove the existence of periodic solutions for a p-Laplacian neutral functional differential equation with multiple deviating arguments
$$ (\varphi_p(x'(t)-c(t)x'(t-r)))' = f(x(t))x'(t)+g(t,x(t),x(t-\tau_1(t)), \dots ,x(t-\tau_{m}(t)))+e(t). $$

Submitted May 17, 2012. Published August 29, 2012.
Math Subject Classifications: 34K15, 34C25
Key Words: Periodic solution; neutral differential equation; deviating argument; p-Laplacian; Mawhin's continuation

Show me the PDF file (233 KB), TEX file, and other files for this article.

Aomar Anane
Université Mohamed I, Faculté des Sciences
Département de Mathématiques et Informatique
Oujda, Maroc
email: anane@sciences.univ-oujda.ac.ma
Omar Chakrone
Université Mohamed I, Faculté des Sciences
Département de Mathématiques et Informatique
Oujda, Maroc
email: chakrone@yahoo.fr
Loubna Moutaouekkil
Université Mohamed I, Faculté des Sciences
Département de Mathématiques et Informatique
Oujda, Maroc
email: loubna_anits@yahoo.fr

Return to the EJDE web page