Tatiana Kavitova
Abstract:
We prove a comparison principle for solutions of the Cauchy problem of the
nonlinear pseudoparabolic equation
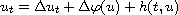 with nonnegative bounded initial data.
We show stabilization of a maximal solution to a maximal solution of
the Cauchy problem for the corresponding ordinary differential
equation
with nonnegative bounded initial data.
We show stabilization of a maximal solution to a maximal solution of
the Cauchy problem for the corresponding ordinary differential
equation
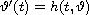 as
as
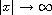 under certain conditions on an initial datum.
under certain conditions on an initial datum.
Submitted March 22, 2012. Published August 20, 2012.
Math Subject Classifications: 35B40, 35B51, 35K70.
Key Words: Pseudoparabolic equation; comparison principle; stabilization.
Show me the PDF file (272 KB), TEX file, and other files for this article.
 |
Tatiana Kavitova Department of Mathematics, Vitebsk State University Moskovskii pr. 33, 210038 Vitebsk, Belarus email: KavitovaTV@tut.by |
|---|
Return to the EJDE web page