Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 136, pp. 1-11.
Boundary behavior of large solutions for semilinear elliptic equations
in borderline cases
Zhijun Zhang
Abstract:
In this article, we analyze the boundary behavior of solutions to
the boundary blow-up elliptic problem
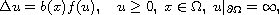
where
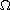 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
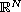 ,
,
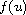 grows slower than any
grows slower than any
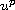 (
(
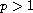 )
at infinity, and
)
at infinity, and
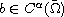 which is non-negative in
which is non-negative in
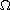 and positive near
and positive near
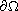 ,
may be vanishing on the boundary.
,
may be vanishing on the boundary.
Submitted June 30, 2012. Published August 19, 2012.
Math Subject Classifications: 35J55, 35J60, 35J65.
Key Words: Semilinear elliptic equations; boundary blow-up;
boundary behavior; borderline cases.
Show me the PDF file (244 KB),
TEX file, and other files for this article.
 |
Zhijun Zhang
School of Mathematics and Information Science
Yantai University
Yantai, Shandong, 264005, China
email: zhangzj@ytu.edu.cn, chinazjzhang@yahoo.com.cn
|
|---|
Return to the EJDE web page
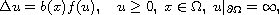
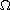 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
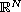 ,
,
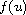 grows slower than any
grows slower than any
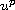 (
(
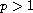 )
at infinity, and
)
at infinity, and
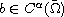 which is non-negative in
which is non-negative in
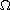 and positive near
and positive near
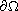 ,
may be vanishing on the boundary.
,
may be vanishing on the boundary.
