Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 135, pp. 1-17.
Positive solutions for a system of second-order boundary-value
problems involving first-order derivatives
Kun Wang, Zhilin Yang
Abstract:
In this article we study the existence and multiplicity of positive
solutions for the system of second-order boundary value problems
involving first order derivatives
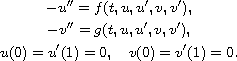
Here
![$f,g\in C([0,1]\times \mathbb{R}_+^{4},
\mathbb{R}_+)(\mathbb{R}_+:=[0,\infty))$](gifs/ab.gif) .
We use fixed point index theory to establish our main results based
on a priori estimates achieved by utilizing Jensen's integral
inequality for concave functions and
.
We use fixed point index theory to establish our main results based
on a priori estimates achieved by utilizing Jensen's integral
inequality for concave functions and
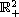 -monotone matrices.
-monotone matrices.
Submitted May 31, 2012. Published August 17, 2012.
Math Subject Classifications: 34B18, 45G15, 45M20, 47H07, 47H11.
Key Words: System of second-order boundary-value problems;
positive solution; first-order derivative;
fixed point index; 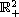 -monotone matrix; concave function.
-monotone matrix; concave function.
Show me the PDF file (277 KB),
TEX file, and other files for this article.
 |
Kun Wang
Department of Mathematics
Qingdao Technological University
Qingdao, 266033, China
email: wangkun880304@163.com
|
|---|
 |
Zhilin Yang
Department of Mathematics
Qingdao Technological University
Qingdao, 266033, China
email: zhilinyang@sina.com
|
|---|
Return to the EJDE web page
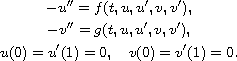
![$f,g\in C([0,1]\times \mathbb{R}_+^{4},
\mathbb{R}_+)(\mathbb{R}_+:=[0,\infty))$](gifs/ab.gif) .
We use fixed point index theory to establish our main results based
on a priori estimates achieved by utilizing Jensen's integral
inequality for concave functions and
.
We use fixed point index theory to establish our main results based
on a priori estimates achieved by utilizing Jensen's integral
inequality for concave functions and
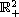 -monotone matrices.
-monotone matrices.

