In this article we study the nonlinear Steklov boundary-value problem
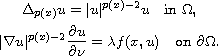
Using the variational method, under appropriate assumptions on f, we obtain results on existence and multiplicity of solutions.
Mostafa Allaoui, Abdel Rachid El Amrouss, Anass Ourraoui
Abstract:
In this article we study the nonlinear Steklov boundary-value problem
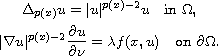
Using the variational method, under appropriate assumptions on f, we obtain
results on existence and multiplicity of solutions.
Submitted February 24, 2012. Published August 15, 2012.
Math Subject Classifications: 35J48, 35J60, 35J66
Key Words: p(x)-Laplace operator; variable exponent Lebesgue space;
variable exponent Sobolev space; Ricceri's variational principle.
Show me the PDF file (252 KB), TEX file, and other files for this article.
 |
Mostafa Allaoui University Mohamed I, Faculty of sciences Department of Mathematics, Oujda, Morocco email: allaoui19@hotmail.com |
|---|---|
 |
Abdel Rachid El Amrouss University Mohamed I, Faculty of sciences Department of Mathematics, Oujda, Morocco email: elamrouss@hotmail.com |
 |
Anass Ourraoui University Mohamed I, Faculty of sciences Department of Mathematics, Oujda, Morocco email: anas.our@hotmail.com |
Return to the EJDE web page