In this note we show that the assumption on the memory term g in Andrade [1] can be modified to be
 ,
where
,
where
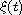 satisfies
satisfies
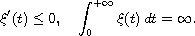
Then we show that rate of decay for the solution is similar to that of the memory term.
Wenjun Liu, Gang Li, Linghui Hong
Abstract:
In this note we show that the assumption on the memory term
g in Andrade [1] can be modified to be
 ,
where
,
where
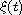 satisfies
satisfies
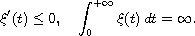
Then we show that rate of decay for the solution is similar to that
of the memory term.
Submitted April 20, 2012. Published August 15, 2012.
Math Subject Classifications: 35L75, 35B40.
Key Words: Rate of decay; plate equation; p-Laplacian; memory term.
Show me the PDF file (180 KB), TEX file, and other files for this article.
 |
Wenjun Liu College of Mathematics and Statistics Nanjing University of Information Science and Technology Nanjing 210044, China email: wjliu@nuist.edu.cn |
|---|---|
 |
Gang Li College of Mathematics and Statistics Nanjing University of Information Science and Technology Nanjing 210044, China email: ligang@nuist.edu.cn |
 |
Linghui Hong College of Mathematics and Statistics Nanjing University of Information Science and Technology Nanjing 210044, China email: hlh3411006@163.com |
Return to the EJDE web page