Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 127, pp. 1-13.
Optimal control problem for a sixth-order Cahn-Hilliard
equation with nonlinear diffusion
Changchun Liu, Zhao Wang
Abstract:
In this article, we study the initial-boundary-value problem for a
sixth-order Cahn-Hilliard type equation
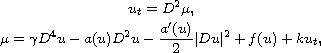
which describes the separation properties of oil-water mixtures,
when a substance enforcing the mixing of the phases is added. The
optimal control of the sixth order Cahn-Hilliard type equation
under boundary condition is given and the existence of optimal
solution to the sixth order Cahn-Hilliard type equation is proved.
Submitted March 1, 2012. Published August 14, 2012.
Math Subject Classifications: 49J20, 35K35, 35K55.
Key Words: Cahn-Hilliard equation; existence; optimal control;
optimal solution.
Show me the PDF file (239 KB),
TEX file, and other files for this article.
 |
Changchun Liu
Department of Mathematics, Jilin University
Changchun 130012, China
email: liucc@jlu.edu.cn
|
|---|
 |
Zhao Wang
Department of Mathematics, Jilin University
Changchun 130012, China
email: wangzhao2717@163.com
|
|---|
Return to the EJDE web page