 -Laplacian
BVPs via homotopic deformations
-Laplacian
BVPs via homotopic deformations
 -Laplacian
BVPs via homotopic deformations
-Laplacian
BVPs via homotopic deformations
Nadir Benkaci, Abdelhamid Benmezai, Johnny Henderson
Abstract:
Under suitable conditions and via homotopic deformation, we provide
existence results for a positive solution to the three-point
 -Laplacian
boundary-value problem
-Laplacian
boundary-value problem
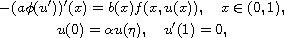
where
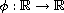 is an increasing homeomorphism
with
is an increasing homeomorphism
with
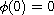 , b does not vanish identically,
and f is continuous.
, b does not vanish identically,
and f is continuous.
Submitted March 12, 2012. Published August 14, 2012.
Math Subject Classifications: 34B15, 34B18.
Key Words: phi-Laplacian BVP; positive solution; fixed point; index theory.
Show me the PDF file (207 KB), TEX file, and other files for this article.
| Nadir Ali Benkaci Faculty of Sciences, University M'Hmed Bouguerra Boumerdes, Algeria email: radians_2005@yahoo.fr | |
 |
Abdelhamid Benmezai Dynamical Systems Laboratory Faculty of Mathematics, USTHB P.O. Box 32 El-Alia Bab-ezouar, Algiers, Algeria email: abenmezai@yahoo.fr |
 |
Johnny Henderson Department of Mathematics, Baylor University Waco, Texas 76798-7328, USA email: Johnny_Henderson@baylor.edu |
Return to the EJDE web page