Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 12, pp. 1-19.
Existence and uniqueness of weak and entropy solutions for
homogeneous Neumann boundary-value problems involving
variable exponents
Bernard K. Bonzi, Ismael Nyanquini, Stanislas Ouaro
Abstract:
In this article we study the nonlinear homogeneous Neumann
boundary-value problem
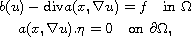
where
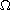 is a smooth bounded open domain in
is a smooth bounded open domain in
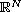 ,
,
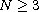 and
and
 the outer
unit normal vector on
the outer
unit normal vector on
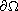 .
We prove the existence
and uniqueness of a weak solution for
.
We prove the existence
and uniqueness of a weak solution for
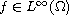 and the existence and uniqueness of an entropy solution for
and the existence and uniqueness of an entropy solution for
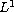 -data
-data
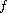 .
The functional setting involves Lebesgue and
Sobolev spaces with variable exponents.
.
The functional setting involves Lebesgue and
Sobolev spaces with variable exponents.
Submitted March 13, 2011. Published January 17, 2012.
Math Subject Classifications: 35J20, 35J25, 35D30, 35B38, 35J60.
Key Words: Elliptic equation; weak solution; entropy solution;
Leray-Lions operator; variable exponent.
Show me the PDF file (325 KB),
TEX file, and other files for this article.
 |
Bernard K. Bonzi
Laboratoire d'Analyse Mathématique des Equations (LAME)
UFR. Sciences Exactes et Appliquées,
Université de Ouagadougou
03 BP 7021 Ouaga 03, Ouagadougou, Burkina Faso
email: bonzib@univ-ouaga.bf
|
|---|
 |
Ismael Nyanquini
Laboratoire d'Analyse Mathématique des Equations (LAME)
Institut des Sciences Exactes et Appliquées
Université Polytechnique de Bobo Dioulasso
01 BP 1091 Bobo-Dioulasso 01,
Bobo Dioulasso, Burkina Faso
email: nyanquis@yahoo.fr
|
|---|
 |
Stanislas Ouaro
Laboratoire d'Analyse Mathématique des Equations (LAME)
UFR. Sciences Exactes et Appliquées,
Université de Ouagadougou
03 BP 7021 Ouaga 03, Ouagadougou, Burkina Faso
email: souaro@univ-ouaga.bf, ouaro@yahoo.fr
|
|---|
Return to the EJDE web page
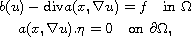
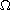 is a smooth bounded open domain in
is a smooth bounded open domain in
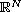 ,
,
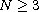 and
and
 the outer
unit normal vector on
the outer
unit normal vector on
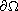 .
We prove the existence
and uniqueness of a weak solution for
.
We prove the existence
and uniqueness of a weak solution for
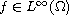 and the existence and uniqueness of an entropy solution for
and the existence and uniqueness of an entropy solution for
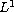 -data
-data
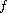 .
The functional setting involves Lebesgue and
Sobolev spaces with variable exponents.
.
The functional setting involves Lebesgue and
Sobolev spaces with variable exponents.


