Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 115, pp. 1-14.
Existence of solutions for Hardy-Sobolev-Maz'ya systems
Jian Wang, Xin Wei
Abstract:
The main goal of this article is to investigate the existence
of solutions for the Hardy-Sobolev-Maz'ya system
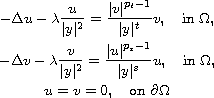
where
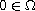 which is a bounded, open and smooth subset of
which is a bounded, open and smooth subset of
 ,
,
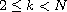 .
The non-existence of classical positive solutions is
obtained by a variational identity and the existence result
by a linking theorem.
.
The non-existence of classical positive solutions is
obtained by a variational identity and the existence result
by a linking theorem.
Submitted December 26, 2011. Published July 5, 2012.
Math Subject Classifications: 35J47, 35J50, 35J57, 58E05.
Key Words: Variational identity; (PS) condition; linking theorem;
Hardy-Sobolev-Maz'ya inequality.
Show me the PDF file (292 KB),
TEX file, and other files for this article.
| |
Jian Wang
Department of Mathematics,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jianwang2007@126.com
|
|---|
 |
Xin Wei
Department of Finance,
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: wxgrat@sohu.com
|
|---|
Return to the EJDE web page
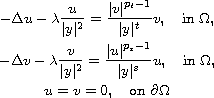
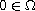 which is a bounded, open and smooth subset of
which is a bounded, open and smooth subset of
 ,
,
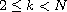 .
The non-existence of classical positive solutions is
obtained by a variational identity and the existence result
by a linking theorem.
.
The non-existence of classical positive solutions is
obtained by a variational identity and the existence result
by a linking theorem.
