Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 109, pp. 1-23.
Existence of bound state solutions for degenerate singular
perturbation problems with sign-changing potentials
Maria J. Alves, Ronaldo B. Assuncao, Paulo C. Carriao, Olimpio H. Miyagaki
Abstract:
In this article, we study the degenerate singular perturbation problems
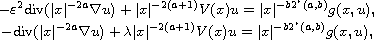
for
 small and
small and
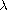 large positive,
where
large positive,
where
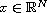 with
with
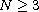 .
We search for solutions that decay to zero as
.
We search for solutions that decay to zero as
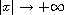 ,
when g is superlinear in the potential function changes signs.
We prove the existence of bound state solutions for degenerate,
singular, semilinear elliptic problems.
Additionally, when the nonlinearity g(x,u) is an odd function of u,
we obtain infinitely many geometrically distinct solutions.
,
when g is superlinear in the potential function changes signs.
We prove the existence of bound state solutions for degenerate,
singular, semilinear elliptic problems.
Additionally, when the nonlinearity g(x,u) is an odd function of u,
we obtain infinitely many geometrically distinct solutions.
Submitted September 22, 2011. Published June 27, 2012.
Math Subject Classifications: 35J20, 35J61, 35J70, 35J75, 35P10, 35P30.
Key Words: Semilinear degenerate elliptic equation; singular perturbation;
variational method; sign-changing potential;
nonlinear Schrodinger equation; bound state solution.
Show me the PDF file (368 KB),
TEX file, and other files for this article.
 |
Maria J. Alves
Departamento de Matemática
Universidade Federal de Minas Gerais, UFMG
Av. Antônio Carlos, 6627, Caixa Postal 702
CEP 30161-970, Belo Horizonte, MG, Brasil
email: mariajose@ufmg.br
|
|---|
 |
Ronaldo B. Assunção
Departamento de Matemática
Universidade Federal de Minas Gerais, UFMG
Av. Antônio Carlos, 6627, Caixa Postal 702
CEP 30161-970, Belo Horizonte, MG, Brasil
email: ronaldo@mat.ufmg.br
|
|---|
 |
Paulo C. Carrião
Departamento de Matemática
Universidade Federal de Minas Gerais, UFMG
Av. Antônio Carlos, 6627, Caixa Postal 702
CEP 30161-970, Belo Horizonte, MG, Brasil
email: carrion@mat.ufmg.br
|
|---|
 |
Olímpio H. Miyagaki
Departamento de Matemática
Universidade Federal de Juiz de Fora, UFJF
Cidade Universitária, Bairro Martelos
CEP 36036-330, Juiz de Fora, MG, Brasil
email: ohmiyagaki@gmail.com
|
|---|
Return to the EJDE web page
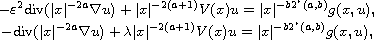
 small and
small and
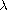 large positive,
where
large positive,
where
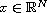 with
with
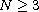 .
We search for solutions that decay to zero as
.
We search for solutions that decay to zero as
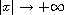 ,
when g is superlinear in the potential function changes signs.
We prove the existence of bound state solutions for degenerate,
singular, semilinear elliptic problems.
Additionally, when the nonlinearity g(x,u) is an odd function of u,
we obtain infinitely many geometrically distinct solutions.
,
when g is superlinear in the potential function changes signs.
We prove the existence of bound state solutions for degenerate,
singular, semilinear elliptic problems.
Additionally, when the nonlinearity g(x,u) is an odd function of u,
we obtain infinitely many geometrically distinct solutions.



