We consider the equation
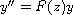 (
(
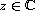 )
with an entire function
)
with an entire function
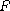 satisfying the condition
satisfying the condition
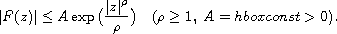
Let
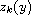 ,
,
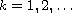 be the zeros of a solution
be the zeros of a solution
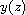 to the above equation. Bounds for the sums
to the above equation. Bounds for the sums
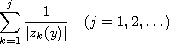
are established. Some applications of these bounds are also considered.
Michael I. Gil'
Abstract:
We consider the equation
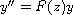 (
(
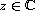 )
with an entire function
)
with an entire function
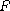 satisfying the condition
satisfying the condition
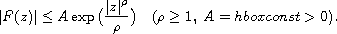
Let
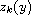 ,
,
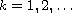 be the zeros of a solution
be the zeros of a solution
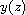 to the above equation. Bounds for the sums
to the above equation. Bounds for the sums
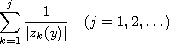
are established. Some applications of these bounds are also considered.
Submitted September 8, 2011. Published June 25, 2012.
Math Subject Classifications: 34C10, 34A30.
Key Words: Complex differential equation; zeros of solutions.
Show me the PDF file (216 KB), TEX file, and other files for this article.
 |
Michael I. Gil' Department of Mathematics Ben Gurion University of the Negev P.0. Box 653, Beer-Sheva 84105, Israel email: gilmi@bezeqint.net |
|---|
Return to the EJDE web page