Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 106, pp. 1-12.
Global continuum and multiple positive solutions to
a p-Laplacian boundary-value problem.
Chan-Gyun Kim, Junping Shi
Abstract:
A p-Laplacian boundary-value problem with positive nonlinearity
is considered. The existence of a continuum of positive solutions
emanating from
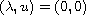 is shown, and it can be extended
to
is shown, and it can be extended
to
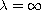 .
Under an additional condition on the nonlinearity,
it is shown that the positive solution is unique for any
.
Under an additional condition on the nonlinearity,
it is shown that the positive solution is unique for any
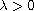 ;
thus the continuum
;
thus the continuum
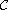 is indeed a continuous curve globally
defined for all
is indeed a continuous curve globally
defined for all
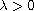 .
In addition, by the upper and lower solutions
method, existence of three positive solutions is established under some
conditions on the nonlinearity.
.
In addition, by the upper and lower solutions
method, existence of three positive solutions is established under some
conditions on the nonlinearity.
Submitted May 25, 2012. Published June 25, 2012.
Math Subject Classifications: 34B18, 34C23, 35J25.
Key Words: Upper and lower solution; positive solution;
p-Laplacian; uniqueness; multiplicity.
Show me the PDF file (258 KB),
TEX file, and other files for this article.
 |
Chan-Gyun Kim
Department of Mathematics, College of William and Mary
Williamsburg, Virginia 23187-8795, USA
email: cgkim75@gmail.com
|
|---|
 |
Junping Shi
Department of Mathematics, College of William and Mary
Williamsburg, Virginia 23187-8795, USA.
School of Mathematical Sciences, Shanxi University
Taiyuan, Shanxi 030006, China
email: shij@math.wm.edu
|
|---|
Return to the EJDE web page
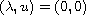 is shown, and it can be extended
to
is shown, and it can be extended
to
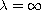 .
Under an additional condition on the nonlinearity,
it is shown that the positive solution is unique for any
.
Under an additional condition on the nonlinearity,
it is shown that the positive solution is unique for any
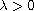 ;
thus the continuum
;
thus the continuum
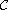 is indeed a continuous curve globally
defined for all
is indeed a continuous curve globally
defined for all
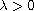 .
In addition, by the upper and lower solutions
method, existence of three positive solutions is established under some
conditions on the nonlinearity.
.
In addition, by the upper and lower solutions
method, existence of three positive solutions is established under some
conditions on the nonlinearity.

