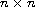Electron. J. Diff. Equ., Vol. 2012 (2012), No. 101, pp. 1-14.

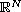
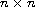Positivity and negativity of solutions to $n\times n$ weighted systems involving the Laplace operator on $\mathbb{R}^N$

Benedicte Alziary, Jacqueline Fleckinger, Marie-Helene Lecureux, Na Wei

Abstract:
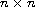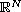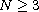We consider the sign of the solutions of a $n\times n$ system defined on the whole space $\mathbb{R}^N$, $N\geq 3$ and a weight function $\rho$ with a positive part decreasing fast enough,
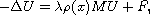
$$ -\Delta U = \lambda \rho(x) MU +F, $$
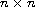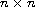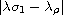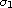where F is a vector of functions, M is a $n\times n$ matrix with constant coefficients, not necessarily cooperative, and the weight function $\rho$ is allowed to change sign. 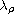We prove that the solutions of the $n\times n$ system exist and then we prove the local fundamental positivity and local fundamental negativity of the solutions when $|\lambda\sigma_1-\lambda_\rho|$ is small enough, where $\sigma_1$ is the largest eigenvalue of the constant matrix M and $\lambda_\rho$ is the "principal" eigenvalue of
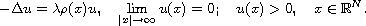
$$ -\Delta u = \lambda \rho(x) u , \quad \lim_{|x|\to \infty} u(x) = 0 ; \quad u(x)>0, \quad x\in \mathbb{R}^N. $$

Submitted February 29, 2012. Published June 15, 2012.
Math Subject Classifications: 35B50, 35J05, 35J47.
Key Words: Elliptic PDE; maximum principle; fundamental positivity; fundamental negativity; indefinite weight, weighted systems.

Show me the PDF file (302 KB), TEX file, and other files for this article.

Bénédicte Alziary
Institut de Mathématique -UMR CNRS 5219- et Ceremath-UT1
Université de Toulouse
31042 Toulouse Cedex, France
email: alziary@univ-tlse1.fr
Jacqueline Fleckinger
Institut de Mathématique -UMR CNRS 5219- et Ceremath-UT1
Université de Toulouse
31042 Toulouse Cedex, France
email: jfleckinger@gmail.com
Marie-Hélène Lecureux
Institut de Mathématique -UMR CNRS 5219- et Ceremath-UT1
Université de Toulouse
31042 Toulouse Cedex, France
email: mhlecureux@gmail.com
Na Wei
Dept. Appl. Math., Northwestern Polytechnical Univ. 710072 Xi'an, China
School of Stat. & Math., Zhongnan Univ. Eco. & Law
430073, Wuhan, China
email: nawei8382@gmail.com

Return to the EJDE web page