We study the unique continuation property for solutions to the quasilinear elliptic equation
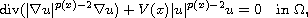
where
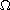 is a smooth bounded domain in
is a smooth bounded domain in
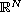 and
and
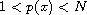 for
for
 in
in
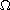 .
.
Johnny Cuadro, Gabriel Lopez
Abstract:
We study the unique continuation property for solutions
to the quasilinear elliptic equation
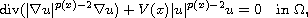
where
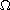 is a smooth bounded domain in
is a smooth bounded domain in
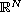 and
and
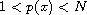 for
for
 in
in
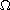 .
.
An addendum was attached on October 14, 2012. It corrects some misprints. See the last page of this article.
Submitted September 8, 2011. Published January 12, 2012.
Math Subject Classifications: 35D05, 35J60, 58E05.
Key Words: p(x)-Laplace operator; unique continuation.
Show me the PDF file (257 KB), TEX file, and other files for this article.
 |
Johnny Cuadro M. Universidad Autónoma Metropolitana Mexico D. F., Mexico email: jcuadrom@yahoo.com |
|---|---|
 |
Gabriel López G. Universidad Autónoma Metropolitana Mexico D. F., Mexico email: jcuadrom@yahoo.com |
Return to the EJDE web page