Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 92, pp. 1-30.
Time-dependent domains for nonlinear evolution operators and
partial differential equations
Chin-Yuan Lin
Abstract:
This article concerns the nonlinear evolution equation
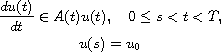
in a real Banach space X, where the nonlinear, time-dependent,
and multi-valued operator
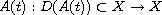 has a time-dependent domain D(A(t)).
It will be shown that, under certain assumptions on A(t),
the equation has a strong solution. Illustrations are
given of solving quasi-linear partial differential equations
of parabolic type with time-dependent boundary conditions.
Those partial differential equations are studied to a
large extent.
has a time-dependent domain D(A(t)).
It will be shown that, under certain assumptions on A(t),
the equation has a strong solution. Illustrations are
given of solving quasi-linear partial differential equations
of parabolic type with time-dependent boundary conditions.
Those partial differential equations are studied to a
large extent.
Submitted June 15, 2011. Published July 18, 2011.
Math Subject Classifications: 47B44, 47H20, 35J25, 35K20.
Key Words: Dissipative operators; evolution equations;
parabolic and elliptic equations.
Show me the PDF file (387 KB),
TEX file, and other files for this article.
 |
Chin-Yuan Lin
Department of Mathematics
National Central University
Chung-Li 320, Taiwan
email: cylin@math.ncu.edu.tw
|
|---|
Return to the EJDE web page
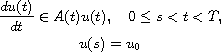
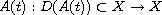 has a time-dependent domain D(A(t)).
It will be shown that, under certain assumptions on A(t),
the equation has a strong solution. Illustrations are
given of solving quasi-linear partial differential equations
of parabolic type with time-dependent boundary conditions.
Those partial differential equations are studied to a
large extent.
has a time-dependent domain D(A(t)).
It will be shown that, under certain assumptions on A(t),
the equation has a strong solution. Illustrations are
given of solving quasi-linear partial differential equations
of parabolic type with time-dependent boundary conditions.
Those partial differential equations are studied to a
large extent.
